Introduction

In this article, we will discuss how to perform an ARIMA forecast on nested data or data that is in a list using R programming language. This is a common scenario in which we have data stored in a list format, where each element of the list corresponds to a different time series. We will use the R programming language, specifically the “forecast” package, to perform the ARIMA forecast.

First, we will need to load the required packages and data. For this example, we will use the “AirPassengers” dataset which is included in the “datasets” package. This dataset contains the number of international airline passengers per month from 1949 to 1960. We will then create a list containing subsets of this data for each year.

library(forecast)

yearly_data <- split(AirPassengers, f = ceiling(seq_along(AirPassengers)/12))

yearly_data

$`1`
 [1] 112 118 132 129 121 135 148 148 136 119 104 118

$`2`
 [1] 115 126 141 135 125 149 170 170 158 133 114 140

$`3`
 [1] 145 150 178 163 172 178 199 199 184 162 146 166

$`4`
 [1] 171 180 193 181 183 218 230 242 209 191 172 194

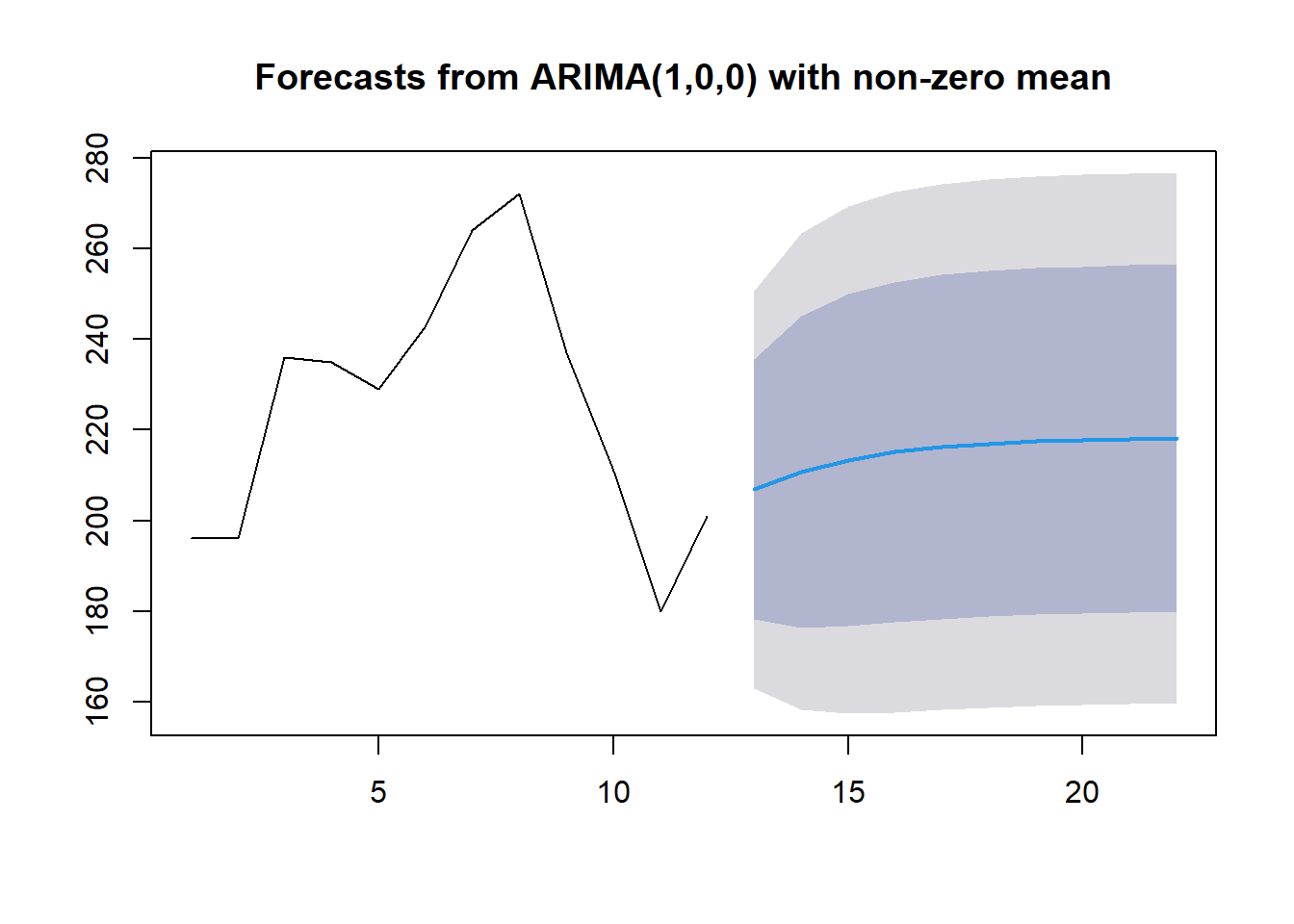
$`5`
 [1] 196 196 236 235 229 243 264 272 237 211 180 201

$`6`
 [1] 204 188 235 227 234 264 302 293 259 229 203 229

$`7`
 [1] 242 233 267 269 270 315 364 347 312 274 237 278

$`8`
 [1] 284 277 317 313 318 374 413 405 355 306 271 306

$`9`
 [1] 315 301 356 348 355 422 465 467 404 347 305 336

$`10`
 [1] 340 318 362 348 363 435 491 505 404 359 310 337

$`11`
 [1] 360 342 406 396 420 472 548 559 463 407 362 405

$`12`
 [1] 417 391 419 461 472 535 622 606 508 461 390 432

In the above code, we use the “split” function to split the data into yearly subsets. The “f” parameter is used to specify the grouping variable which, in this case, is the sequence of numbers from 1 to the length of the dataset divided by 12, rounded up to the nearest integer. This creates a list of 12 elements, one for each year.

Function

Next, we will define a function that takes a single element of the list, fits an ARIMA model, and generates a forecast.

arima_forecast <- function(x){
  fit <- auto.arima(x)
  forecast(fit)
}

This function takes a single argument “x” which is one of the elements of the list. We use the “auto.arima” function from the “forecast” package to fit an ARIMA model to the data. The “forecast” function is then used to generate a forecast based on this model.

Example

We can now use the “lapply” function to apply this function to each element of the list.

forecasts <- lapply(yearly_data, arima_forecast)

The “lapply” function applies the “arima_forecast” function to each element of the “yearly_data” list and returns a list of forecasts.

Finally, we can extract and plot the forecasts for a specific year.

plot(forecasts[[5]])

Now lets take a look at them all.

par(mfrow = c(2,1))

purrr::map(forecasts, plot)

$`1`
$`1`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 132.2237 126.4744 126.4744 126.4744 126.4744 126.4744 126.4744 126.4744
 [9] 126.4744 126.4744

$`1`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 120.1608 113.7751
14 110.0828 101.4056
15 110.0828 101.4056
16 110.0828 101.4056
17 110.0828 101.4056
18 110.0828 101.4056
19 110.0828 101.4056
20 110.0828 101.4056
21 110.0828 101.4056
22 110.0828 101.4056

$`1`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 144.2865 150.6722
14 142.8660 151.5432
15 142.8660 151.5432
16 142.8660 151.5432
17 142.8660 151.5432
18 142.8660 151.5432
19 142.8660 151.5432
20 142.8660 151.5432
21 142.8660 151.5432
22 142.8660 151.5432


$`2`
$`2`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 153.8708 139.5919 139.5919 139.5919 139.5919 139.5919 139.5919 139.5919
 [9] 139.5919 139.5919

$`2`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 136.3778 127.1175
14 115.8789 103.3260
15 115.8789 103.3260
16 115.8789 103.3260
17 115.8789 103.3260
18 115.8789 103.3260
19 115.8789 103.3260
20 115.8789 103.3260
21 115.8789 103.3260
22 115.8789 103.3260

$`2`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 171.3638 180.6240
14 163.3048 175.8577
15 163.3048 175.8577
16 163.3048 175.8577
17 163.3048 175.8577
18 163.3048 175.8577
19 163.3048 175.8577
20 163.3048 175.8577
21 163.3048 175.8577
22 163.3048 175.8577


$`3`
$`3`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 173.6413 170.0479 170.0479 170.0479 170.0479 170.0479 170.0479 170.0479
 [9] 170.0479 170.0479

$`3`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 153.5404 142.8995
14 146.6452 134.2565
15 146.6452 134.2565
16 146.6452 134.2565
17 146.6452 134.2565
18 146.6452 134.2565
19 146.6452 134.2565
20 146.6452 134.2565
21 146.6452 134.2565
22 146.6452 134.2565

$`3`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 193.7423 204.3831
14 193.4506 205.8393
15 193.4506 205.8393
16 193.4506 205.8393
17 193.4506 205.8393
18 193.4506 205.8393
19 193.4506 205.8393
20 193.4506 205.8393
21 193.4506 205.8393
22 193.4506 205.8393


$`4`
$`4`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 194.0074 194.0119 194.0147 194.0164 194.0174 194.0180 194.0184 194.0186
 [9] 194.0187 194.0188

$`4`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 169.7973 156.9812
14 165.6741 150.6730
15 164.2944 148.5614
16 163.8005 147.8051
17 163.6201 147.5288
18 163.5539 147.4272
19 163.5296 147.3898
20 163.5207 147.3761
21 163.5175 147.3711
22 163.5163 147.3692

$`4`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 218.2176 231.0336
14 222.3497 237.3509
15 223.7350 239.4680
16 224.2322 240.2276
17 224.4146 240.5059
18 224.4821 240.6088
19 224.5071 240.6469
20 224.5165 240.6611
21 224.5200 240.6664
22 224.5213 240.6684


$`5`
$`5`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 206.8929 210.7977 213.3851 215.0996 216.2356 216.9884 217.4872 217.8178
 [9] 218.0368 218.1819

$`5`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 178.2600 163.1026
14 176.4492 158.2662
15 176.8082 157.4455
16 177.5860 157.7275
17 178.3181 158.2458
18 178.8949 158.7294
19 179.3167 159.1104
20 179.6134 159.3893
21 179.8176 159.5856
22 179.9562 159.7208

$`5`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 235.5258 250.6831
14 245.1461 263.3291
15 249.9620 269.3246
16 252.6131 272.4716
17 254.1531 274.2255
18 255.0819 275.2475
19 255.6578 275.8641
20 256.0221 276.2462
21 256.2559 276.4879
22 256.4076 276.6430


$`6`
$`6`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 245.0709 240.0400 240.0400 240.0400 240.0400 240.0400 240.0400 240.0400
 [9] 240.0400 240.0400

$`6`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 212.6687 195.5160
14 196.9893 174.1996
15 196.9893 174.1996
16 196.9893 174.1996
17 196.9893 174.1996
18 196.9893 174.1996
19 196.9893 174.1996
20 196.9893 174.1996
21 196.9893 174.1996
22 196.9893 174.1996

$`6`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 277.4731 294.6259
14 283.0907 305.8803
15 283.0907 305.8803
16 283.0907 305.8803
17 283.0907 305.8803
18 283.0907 305.8803
19 283.0907 305.8803
20 283.0907 305.8803
21 283.0907 305.8803
22 283.0907 305.8803


$`7`
$`7`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 278.0001 278.0001 278.0002 278.0002 278.0002 278.0002 278.0002 278.0002
 [9] 278.0002 278.0002

$`7`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 236.8903 215.1282
14 228.5879 202.4307
15 225.3145 197.4243
16 223.9224 195.2953
17 223.3147 194.3659
18 223.0466 193.9559
19 222.9278 193.7742
20 222.8751 193.6936
21 222.8516 193.6577
22 222.8412 193.6418

$`7`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 319.1098 340.8720
14 327.4123 353.5695
15 330.6859 358.5760
16 332.0780 360.7051
17 332.6857 361.6345
18 332.9538 362.0445
19 333.0726 362.2262
20 333.1254 362.3069
21 333.1488 362.3427
22 333.1592 362.3587


$`8`
$`8`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 349.0540 373.2678 369.7906 348.0549 325.4487 315.1915 319.8599 332.7645
 [9] 344.2812 348.1670

$`8`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 315.6225 297.9249
14 322.1404 295.0752
15 314.7795 285.6584
16 292.8344 263.6024
17 266.5768 235.4118
18 252.9822 220.0505
19 257.0954 223.8699
20 269.7958 236.4622
21 280.1875 246.2583
22 283.2781 248.9280

$`8`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 382.4855 400.1831
14 424.3952 451.4604
15 424.8018 453.9229
16 403.2754 432.5074
17 384.3206 415.4855
18 377.4009 410.3325
19 382.6243 415.8498
20 395.7332 429.0668
21 408.3750 442.3042
22 413.0559 447.4061


$`9`
$`9`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 378.9729 406.5723 408.7509 392.6048 372.9147 361.5778 362.0569 370.2398
 [9] 379.1516 383.6927

$`9`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 336.2126 313.5766
14 342.0963 307.9648
15 339.3660 302.6358
16 323.1265 286.3469
17 300.2319 261.7560
18 285.7363 245.5882
19 285.5516 245.0521
20 293.6654 253.1294
21 301.8675 260.9558
22 305.8147 264.5885

$`9`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 421.7333 444.3692
14 471.0482 505.1797
15 478.1359 514.8660
16 462.0831 498.8627
17 445.5975 484.0734
18 437.4193 477.5674
19 438.5622 479.0617
20 446.8142 487.3503
21 456.4356 497.3473
22 461.5707 502.7968


$`10`
$`10`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 391.9249 381.5489 381.5489 381.5489 381.5489 381.5489 381.5489 381.5489
 [9] 381.5489 381.5489

$`10`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 331.8921 300.1126
14 304.6704 263.9734
15 304.6704 263.9734
16 304.6704 263.9734
17 304.6704 263.9734
18 304.6704 263.9734
19 304.6704 263.9734
20 304.6704 263.9734
21 304.6704 263.9734
22 304.6704 263.9734

$`10`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 451.9577 483.7372
14 458.4274 499.1244
15 458.4274 499.1244
16 458.4274 499.1244
17 458.4274 499.1244
18 458.4274 499.1244
19 458.4274 499.1244
20 458.4274 499.1244
21 458.4274 499.1244
22 458.4274 499.1244


$`11`
$`11`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 408.4203 410.7762 412.3990 413.5168 414.2868 414.8171 415.1824 415.4340
 [9] 415.6074 415.7268

$`11`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 342.2241 307.1820
14 330.3960 287.8452
15 326.1006 280.4170
16 324.5481 277.4509
17 324.0788 276.3255
18 324.0270 275.9656
19 324.1175 275.9106
20 324.2390 275.9632
21 324.3506 276.0422
22 324.4407 276.1168

$`11`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 474.6165 509.6586
14 491.1565 533.7072
15 498.6974 544.3810
16 502.4855 549.5827
17 504.4948 552.2480
18 505.6072 553.6686
19 506.2474 554.4543
20 506.6291 554.9049
21 506.8641 555.1726
22 507.0128 555.3367


$`12`
$`12`$mean
Time Series:
Start = 13 
End = 22 
Frequency = 1 
 [1] 502.9998 476.0531 476.0531 476.0531 476.0531 476.0531 476.0531 476.0531
 [9] 476.0531 476.0531

$`12`$lower
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 437.2687 402.4728
14 387.1722 340.1214
15 387.1722 340.1214
16 387.1722 340.1214
17 387.1722 340.1214
18 387.1722 340.1214
19 387.1722 340.1214
20 387.1722 340.1214
21 387.1722 340.1214
22 387.1722 340.1214

$`12`$upper
Time Series:
Start = 13 
End = 22 
Frequency = 1 
        80%      95%
13 568.7308 603.5267
14 564.9341 611.9848
15 564.9341 611.9848
16 564.9341 611.9848
17 564.9341 611.9848
18 564.9341 611.9848
19 564.9341 611.9848
20 564.9341 611.9848
21 564.9341 611.9848
22 564.9341 611.9848

dev.off()

null device 
          1

Voila!