Estimate F Distribution Parameters
Arguments
- .x
The vector of data to be passed to the function, where the data comes from the
rf()function.- .auto_gen_empirical
This is a boolean value of TRUE/FALSE with default set to TRUE. This will automatically create the
tidy_empirical()output for the.xparameter and use thetidy_combine_distributions(). The user can then plot out the data using$combined_data_tblfrom the function output.
Details
This function will attempt to estimate the F distribution parameters
given some vector of values produced by rf(). The estimation method
is from the NIST Engineering Statistics Handbook.
See also
Other Parameter Estimation:
util_bernoulli_param_estimate(),
util_beta_param_estimate(),
util_binomial_param_estimate(),
util_burr_param_estimate(),
util_cauchy_param_estimate(),
util_chisquare_param_estimate(),
util_exponential_param_estimate(),
util_gamma_param_estimate(),
util_generalized_beta_param_estimate(),
util_generalized_pareto_param_estimate(),
util_geometric_param_estimate(),
util_hypergeometric_param_estimate(),
util_inverse_burr_param_estimate(),
util_inverse_pareto_param_estimate(),
util_inverse_weibull_param_estimate(),
util_logistic_param_estimate(),
util_lognormal_param_estimate(),
util_negative_binomial_param_estimate(),
util_normal_param_estimate(),
util_paralogistic_param_estimate(),
util_pareto1_param_estimate(),
util_pareto_param_estimate(),
util_poisson_param_estimate(),
util_t_param_estimate(),
util_triangular_param_estimate(),
util_uniform_param_estimate(),
util_weibull_param_estimate(),
util_zero_truncated_binomial_param_estimate(),
util_zero_truncated_geometric_param_estimate(),
util_zero_truncated_negative_binomial_param_estimate(),
util_zero_truncated_poisson_param_estimate()
Other F Distribution:
tidy_f(),
util_f_stats_tbl()
Examples
library(dplyr)
library(ggplot2)
set.seed(123)
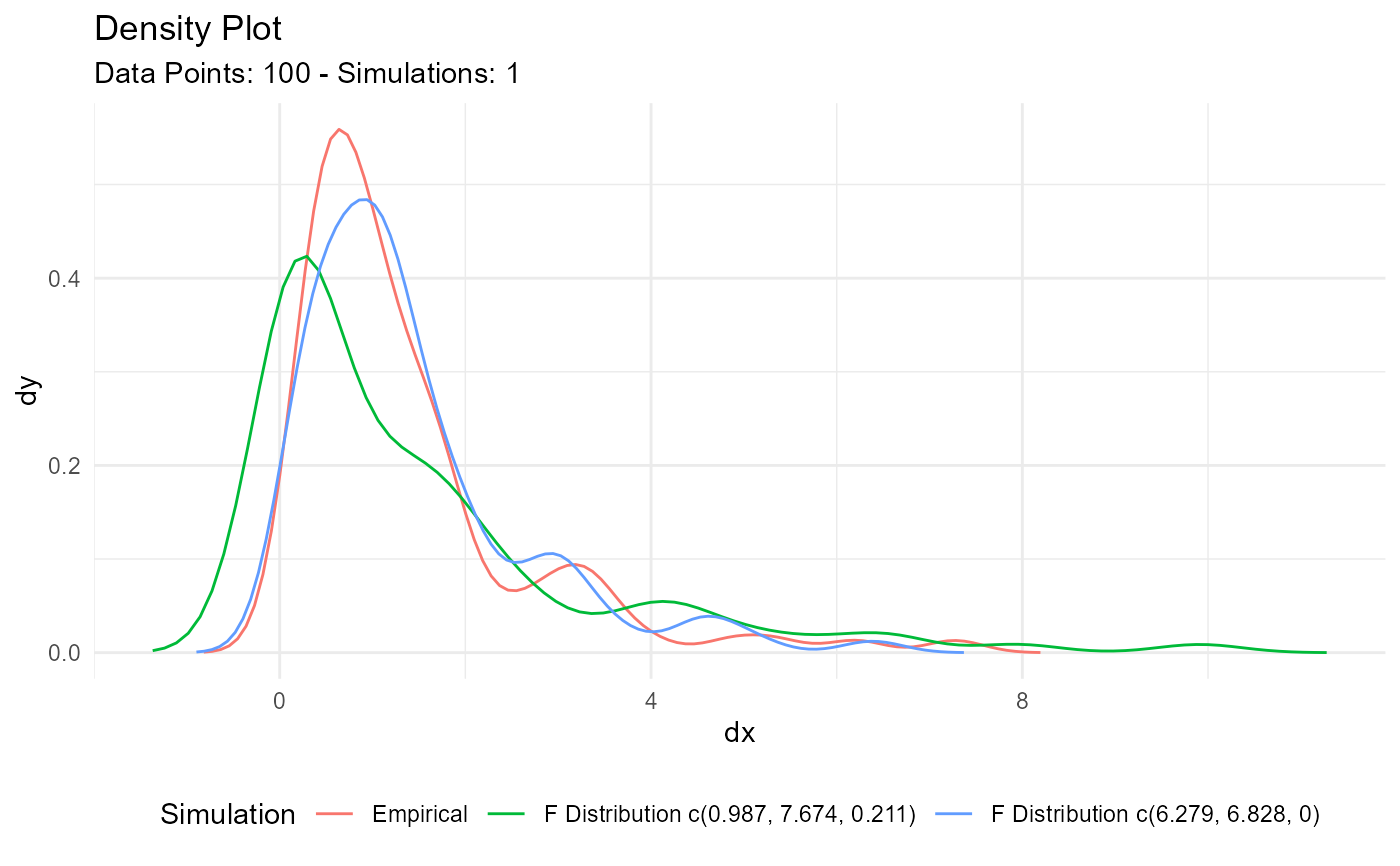
x <- rf(100, df1 = 5, df2 = 10, ncp = 1)
output <- util_f_param_estimate(x)
output$parameter_tbl
#> # A tibble: 2 × 10
#> dist_type samp_size min max mean variance method df1_est df2_est ncp_est
#> <chr> <int> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl> <dbl>
#> 1 F Distrib… 100 0.105 7.27 1.38 1.67 MME 0.987 7.67 0.211
#> 2 F Distrib… 100 0.105 7.27 1.38 1.67 MLE 6.28 6.83 0
output$combined_data_tbl |>
tidy_combined_autoplot()